#include <constitutive_laws.h>
 Inheritance diagram for oomph::GeneralisedHookean:
Inheritance diagram for oomph::GeneralisedHookean:Public Member Functions | |
| GeneralisedHookean (double *nu_pt, double *e_pt) | |
| GeneralisedHookean (double *nu_pt) | |
| virtual | ~GeneralisedHookean () |
| Virtual destructor. More... | |
| void | calculate_second_piola_kirchhoff_stress (const DenseMatrix< double > &g, const DenseMatrix< double > &G, DenseMatrix< double > &sigma) |
| Calculate the contravariant 2nd Piola Kirchhoff stress tensor. Arguments are the covariant undeformed and deformed metric tensor and the matrix in which to return the stress tensor. More... | |
| void | calculate_second_piola_kirchhoff_stress (const DenseMatrix< double > &g, const DenseMatrix< double > &G, DenseMatrix< double > &sigma_dev, DenseMatrix< double > &G_contra, double &Gdet) |
Calculate the deviatoric part 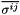 of the contravariant 2nd Piola Kirchhoff stress tensor of the contravariant 2nd Piola Kirchhoff stress tensor 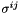 . Also return the contravariant deformed metric tensor and the determinant of the deformed metric tensor. This form is appropriate for truly-incompressible materials for which . Also return the contravariant deformed metric tensor and the determinant of the deformed metric tensor. This form is appropriate for truly-incompressible materials for which 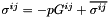 where the "pressure" where the "pressure" 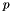 is determined by is determined by 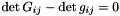 . More... . More... | |
| void | calculate_second_piola_kirchhoff_stress (const DenseMatrix< double > &g, const DenseMatrix< double > &G, DenseMatrix< double > &sigma_dev, DenseMatrix< double > &Gcontra, double &gen_dil, double &inv_kappa) |
Calculate the deviatoric part of the contravariant 2nd Piola Kirchoff stress tensor. Also return the contravariant deformed metric tensor, the generalised dilatation, 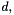 and the inverse of the bulk modulus and the inverse of the bulk modulus 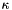 . This form is appropriate for near-incompressible materials for which . This form is appropriate for near-incompressible materials for which 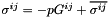 where the "pressure" where the "pressure" 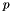 is determined from is determined from 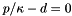 . More... . More... | |
| bool | requires_incompressibility_constraint () |
| Pure virtual function in which the writer must declare if the constitutive equation requires an incompressible formulation in which the volume constraint is enforced explicitly. Used as a sanity check in PARANOID mode. False. More... | |
 Public Member Functions inherited from oomph::ConstitutiveLaw Public Member Functions inherited from oomph::ConstitutiveLaw | |
| ConstitutiveLaw () | |
| Empty constructor. More... | |
| virtual | ~ConstitutiveLaw () |
| Empty virtual destructor. More... | |
| virtual void | calculate_d_second_piola_kirchhoff_stress_dG (const DenseMatrix< double > &g, const DenseMatrix< double > &G, const DenseMatrix< double > &sigma, RankFourTensor< double > &d_sigma_dG, const bool &symmetrize_tensor=true) |
| Calculate the derivatives of the contravariant 2nd Piola Kirchhoff stress tensor with respect to the deformed metric tensor. Arguments are the covariant undeformed and deformed metric tensor, the current value of the stress tensor and the rank four tensor in which to return the derivatives of the stress tensor The default implementation uses finite differences, but can be overloaded for constitutive laws in which an analytic formulation is possible. If the boolean flag symmetrize_tensor is false, only the "upper triangular" entries of the tensor will be filled in. This is a useful efficiency when using the derivatives in Jacobian calculations. More... | |
| virtual void | calculate_d_second_piola_kirchhoff_stress_dG (const DenseMatrix< double > &g, const DenseMatrix< double > &G, const DenseMatrix< double > &sigma, const double &detG, const double &interpolated_solid_p, RankFourTensor< double > &d_sigma_dG, DenseMatrix< double > &d_detG_dG, const bool &symmetrize_tensor=true) |
Calculate the derivatives of the contravariant 2nd Piola Kirchhoff stress tensor 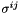 . with respect to the deformed metric tensor. Also return the derivatives of the determinant of the deformed metric tensor with respect to the deformed metric tensor. This form is appropriate for truly-incompressible materials. The default implementation uses finite differences for the derivatives that depend on the constitutive law, but not for the derivatives of the determinant, which are generic. More... . with respect to the deformed metric tensor. Also return the derivatives of the determinant of the deformed metric tensor with respect to the deformed metric tensor. This form is appropriate for truly-incompressible materials. The default implementation uses finite differences for the derivatives that depend on the constitutive law, but not for the derivatives of the determinant, which are generic. More... | |
| virtual void | calculate_d_second_piola_kirchhoff_stress_dG (const DenseMatrix< double > &g, const DenseMatrix< double > &G, const DenseMatrix< double > &sigma, const double &gen_dil, const double &inv_kappa, const double &interpolated_solid_p, RankFourTensor< double > &d_sigma_dG, DenseMatrix< double > &d_gen_dil_dG, const bool &symmetrize_tensor=true) |
Calculate the derivatives of the contravariant 2nd Piola Kirchoff stress tensor with respect to the deformed metric tensor. Also return the derivatives of the generalised dilatation, 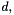 with respect to the deformed metric tensor. This form is appropriate for near-incompressible materials. The default implementation uses finite differences. If the boolean flag symmetrize_tensor is false, only the "upper triangular" entries of the tensor will be filled in. This is a useful efficiency when using the derivatives in Jacobian calculations. More... with respect to the deformed metric tensor. This form is appropriate for near-incompressible materials. The default implementation uses finite differences. If the boolean flag symmetrize_tensor is false, only the "upper triangular" entries of the tensor will be filled in. This is a useful efficiency when using the derivatives in Jacobian calculations. More... | |
Private Attributes | |
| double * | Nu_pt |
| Poisson ratio. More... | |
| double * | E_pt |
| Young's modulus. More... | |
| bool | Must_delete_e |
| Boolean flag to indicate if storage for elastic modulus must be deleted in destructor. More... | |
Additional Inherited Members | |
 Protected Member Functions inherited from oomph::ConstitutiveLaw Protected Member Functions inherited from oomph::ConstitutiveLaw | |
| bool | is_matrix_square (const DenseMatrix< double > &M) |
| Test whether a matrix is square. More... | |
| bool | are_matrices_of_equal_dimensions (const DenseMatrix< double > &M1, const DenseMatrix< double > &M2) |
| Test whether two matrices are of equal dimensions. More... | |
| void | error_checking_in_input (const DenseMatrix< double > &g, const DenseMatrix< double > &G, DenseMatrix< double > &sigma) |
| Check for errors in the input, i.e. check that the dimensions of the arrays are all consistent. More... | |
| double | calculate_contravariant (const DenseMatrix< double > &Gcov, DenseMatrix< double > &Gcontra) |
| Calculate a contravariant tensor from a covariant tensor, and return the determinant of the covariant tensor. More... | |
| void | calculate_d_contravariant_dG (const DenseMatrix< double > &Gcov, RankFourTensor< double > &dGcontra_dG, DenseMatrix< double > &d_detG_dG) |
| Calculate the derivatives of the contravariant tensor and the derivatives of the determinant of the covariant tensor with respect to the components of the covariant tensor. More... | |
Detailed Description
Class for a "non-rational" extension of classical linear elasticity to large displacements:
![\[ \sigma^{ij} = E^{ijkl} \gamma_{kl} \]](form_143.png)
where
![\[ E^{ijkl} = \frac{E}{(1+\nu)} \left( \frac{\nu}{(1-2\nu)} G^{ij} G^{kl} + \frac{1}{2} \left( G^{ik} G^{jl} + G^{il} G^{jk} \right) \right) \]](form_144.png)
For small strains 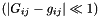 this approaches the version appropriate for linear elasticity, obtained by replacing
this approaches the version appropriate for linear elasticity, obtained by replacing 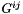 with
with 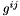 .
.
We provide three versions of calculate_second_piola_kirchhoff_stress():
- If
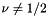 (and not close to
(and not close to 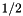 ), the constitutive law can be used directly in the above form, using the deformed and undeformed metric tensors as input.
), the constitutive law can be used directly in the above form, using the deformed and undeformed metric tensors as input. - If the material is incompressible (
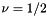 ), the first term in the above expression for
), the first term in the above expression for 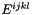 is singular. We re-write the constitutive equation for this case as
is singular. We re-write the constitutive equation for this case as
where the pressure![\[ \sigma^{ij} = -p G^{ij} + \frac{E}{3} \left( G^{ik} G^{jl} + G^{il} G^{jk} \right) \gamma_{kl} \]](form_152.png)
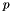 needs to be determined independently via the incompressibility constraint. In this case, the stress returned by
needs to be determined independently via the incompressibility constraint. In this case, the stress returned by calculate_second_piola_kirchhoff_stress()contains only the deviatoric part of the 2nd Piola Kirchhoff stress,
The function also returns the contravariant metric tensor![\[ \overline{\sigma}^{ij} = \frac{E}{3} \left( G^{ik} G^{jl} + G^{il} G^{jk} \right) \gamma_{kl}. \]](form_153.png)
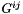 (since it is needed to form the complete stress tensor), and the determinant of the deformed covariant metric tensor
(since it is needed to form the complete stress tensor), and the determinant of the deformed covariant metric tensor 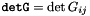 (since it is needed in the equation that enforces the incompressibility).
(since it is needed in the equation that enforces the incompressibility). - If
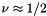 , the original form of the constitutive equation could be used, but the resulting equations tend to be ill-conditioned since they contain the product of the large "bulk modulus"
, the original form of the constitutive equation could be used, but the resulting equations tend to be ill-conditioned since they contain the product of the large "bulk modulus"
and the small "generalised dilatation"![\[ \kappa = \frac{E\nu}{(1+\nu)(1-2\nu)} \]](form_156.png)
[![\[ d = \frac{1}{2} G^{ij} (G_{ij}-g_{ij}). \]](form_157.png)
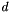 represents the actual dilatation in the small strain limit; for large deformations it doesn't have any sensible interpretation (or does it?). It is simply the term that needs to go to zero as
represents the actual dilatation in the small strain limit; for large deformations it doesn't have any sensible interpretation (or does it?). It is simply the term that needs to go to zero as 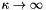 .] In this case, the stress returned by
.] In this case, the stress returned by calculate_second_piola_kirchhoff_stress()contains only the deviatoric part of the 2nd Piola Kirchhoff stress,
The function also returns the contravariant metric tensor![\[ \overline{\sigma}^{ij} = \frac{E}{3} \left( G^{ik} G^{jl} + G^{il} G^{jk} \right) \gamma_{kl}. \]](form_153.png)
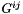 (since it is needed to form the complete stress tensor), the inverse of the bulk modulus, and the generalised dilatation (since they are needed in the equation that determines the pressure).
(since it is needed to form the complete stress tensor), the inverse of the bulk modulus, and the generalised dilatation (since they are needed in the equation that determines the pressure).
Definition at line 714 of file constitutive_laws.h.
Constructor & Destructor Documentation
◆ GeneralisedHookean() [1/2]
|
inline |
The constructor takes the pointers to values of material parameters: Poisson's ratio and Young's modulus.
Definition at line 721 of file constitutive_laws.h.
◆ GeneralisedHookean() [2/2]
|
inline |
The constructor takes the pointers to value of Poisson's ratio . Young's modulus is set to E=1.0, implying that all stresses have been non-dimensionalised on on it.
Definition at line 729 of file constitutive_laws.h.
◆ ~GeneralisedHookean()
|
inlinevirtual |
Virtual destructor.
Definition at line 735 of file constitutive_laws.h.
Member Function Documentation
◆ calculate_second_piola_kirchhoff_stress() [1/3]
|
virtual |
Calculate the contravariant 2nd Piola Kirchhoff stress tensor. Arguments are the covariant undeformed and deformed metric tensor and the matrix in which to return the stress tensor.
Calculate the contravariant 2nd Piola Kirchhoff stress tensor. Arguments are the covariant undeformed (stress-free) and deformed metric tensors, g and G, and the matrix in which to return the stress tensor.
Implements oomph::ConstitutiveLaw.
Definition at line 673 of file constitutive_laws.cc.
References oomph::ConstitutiveLaw::calculate_contravariant(), oomph::ConstitutiveLaw::error_checking_in_input(), i, and oomph::DenseMatrix< T >::nrow().
Referenced by oomph::ConstitutiveLaw::calculate_d_second_piola_kirchhoff_stress_dG(), and calculate_second_piola_kirchhoff_stress().
◆ calculate_second_piola_kirchhoff_stress() [2/3]
|
virtual |
Calculate the deviatoric part 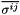 of the contravariant 2nd Piola Kirchhoff stress tensor
of the contravariant 2nd Piola Kirchhoff stress tensor 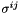 . Also return the contravariant deformed metric tensor and the determinant of the deformed metric tensor. This form is appropriate for truly-incompressible materials for which
. Also return the contravariant deformed metric tensor and the determinant of the deformed metric tensor. This form is appropriate for truly-incompressible materials for which 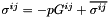 where the "pressure"
where the "pressure" 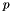 is determined by
is determined by 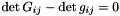 .
.
Calculate the deviatoric part 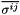 of the contravariant 2nd Piola Kirchhoff stress tensor
of the contravariant 2nd Piola Kirchhoff stress tensor 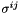 . Also return the contravariant deformed metric tensor and the determinant of the deformed metric tensor. This form is appropriate for truly-incompressible materials for which
. Also return the contravariant deformed metric tensor and the determinant of the deformed metric tensor. This form is appropriate for truly-incompressible materials for which 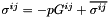 where the "pressure"
where the "pressure" 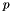 is determined by
is determined by 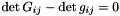 .
.
Reimplemented from oomph::ConstitutiveLaw.
Definition at line 801 of file constitutive_laws.cc.
References oomph::ConstitutiveLaw::calculate_contravariant(), oomph::IsotropicStrainEnergyFunctionConstitutiveLaw::calculate_second_piola_kirchhoff_stress(), oomph::ConstitutiveLaw::error_checking_in_input(), i, and oomph::DenseMatrix< T >::nrow().
◆ calculate_second_piola_kirchhoff_stress() [3/3]
|
virtual |
Calculate the deviatoric part of the contravariant 2nd Piola Kirchoff stress tensor. Also return the contravariant deformed metric tensor, the generalised dilatation, 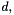 and the inverse of the bulk modulus
and the inverse of the bulk modulus 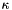 . This form is appropriate for near-incompressible materials for which
. This form is appropriate for near-incompressible materials for which 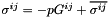 where the "pressure"
where the "pressure" 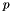 is determined from
is determined from 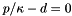 .
.
Calculate the deviatoric part of the contravariant 2nd Piola Kirchoff stress tensor. Also return the contravariant deformed metric tensor, the generalised dilatation, 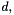 and the inverse of the bulk modulus
and the inverse of the bulk modulus 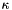 . This form is appropriate for near-incompressible materials for which
. This form is appropriate for near-incompressible materials for which 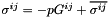 where the "pressure"
where the "pressure" 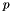 is determined from
is determined from 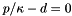 .
.
Reimplemented from oomph::ConstitutiveLaw.
Definition at line 755 of file constitutive_laws.cc.
References oomph::ConstitutiveLaw::calculate_second_piola_kirchhoff_stress(), calculate_second_piola_kirchhoff_stress(), i, and oomph::DenseMatrix< T >::nrow().
◆ requires_incompressibility_constraint()
|
inlinevirtual |
Pure virtual function in which the writer must declare if the constitutive equation requires an incompressible formulation in which the volume constraint is enforced explicitly. Used as a sanity check in PARANOID mode. False.
Implements oomph::ConstitutiveLaw.
Definition at line 783 of file constitutive_laws.h.
Member Data Documentation
◆ E_pt
|
private |
Young's modulus.
Definition at line 791 of file constitutive_laws.h.
◆ Must_delete_e
|
private |
Boolean flag to indicate if storage for elastic modulus must be deleted in destructor.
Definition at line 795 of file constitutive_laws.h.
◆ Nu_pt
|
private |
Poisson ratio.
Definition at line 788 of file constitutive_laws.h.
The documentation for this class was generated from the following files: