Go to the source code of this file.
Classes | |
| class | oomph::PseudoBucklingRing |
| Pseudo buckling ring: Circular ring deformed by the N-th buckling mode of a thin-wall elastic ring.
where A is the ratio of the aziumuthal to the radial buckling amplitude (A=-1/N for statically buckling rings) and epsilon is the buckling amplitude. More... | |
| class | oomph::PseudoBucklingRingElement |
| Pseudo buckling ring: Circular ring deformed by the N-th buckling mode of a thin-wall elastic ring.
where A is the ratio of the aziumuthal to the radial buckling amplitude (A=-1/N for statically buckling rings) and epsilon is the buckling amplitude. Scale R_0 is adjusted to ensure conservation of (computational) volume/area. This is implemented by a pseudo-elasticity approach: The governing equation for
The pointer to the reference pressure needs to be set with reference_pressure_pt(). More... | |
Namespaces | |
| oomph | |
![\[ x = R_0 \cos(\zeta) + \epsilon \left( \cos(N \zeta) \cos(\zeta) - A \sin(N \zeta) \sin(\zeta) \right) sin(2 \pi t/T) \]](form_347.png)
![\[ y = R_0 \sin(\zeta) + \epsilon \left( \cos(N \zeta) \sin(\zeta) + A \sin(N \zeta) \cos(\zeta) \right) sin(2 \pi t/T) \]](form_348.png)
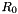 is:
is: ![\[ p_{ref} = R_0 - 1.0 \]](form_349.png)